Units of Measurement and Dimensional Analysis!

Units of Measurement:
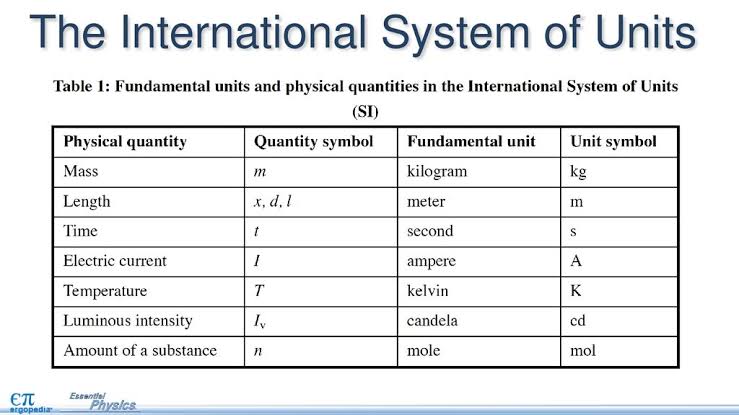
- Definition: Standardized quantities used to express physical quantities.
- Importance: Ensures accurate communication and analysis.
- Examples: Length (meter), time (second), mass (kilogram).
Dimensional Analysis:
- Definition: Method to check consistency of equations and calculations.
- Importance: Identifies errors and ensures balanced equations.
- Steps: Examine dimensions (units) of quantities involved.

Unit Conversion:
- Definition: Converting between different units of measurement.
- Method: Use conversion factors to multiply or divide original value.
- Example: Converting meters to feet: 1 meter = 3.28 feet.

Question and Answer:
- What’s the deal with units of measurement?
Units of measurement help us express and understand physical quantities in a standardized way. - How do I figure out which unit to use for a measurement?
The unit depends on what you’re measuring. For example, length is measured in meters, while time is measured in seconds. - What’s the point of dimensional analysis in science?
Dimensional analysis helps us check the consistency and accuracy of equations by examining the units involved. - How can I convert between different units of measurement?
You can convert between units using conversion factors, which represent the relationship between different units. - Any handy conversion factors I should know?
Sure! Some common conversion factors include 1 meter = 3.28 feet, 1 kilogram = 2.20 pounds, and 1 liter = 0.26 gallons. - Why should I bother checking the dimensions of quantities in equations?
Checking dimensions ensures that equations make sense and are balanced. If the dimensions don’t match, there might be an error. - Can dimensional analysis be used outside of science?
Absolutely! Dimensional analysis can be applied in engineering, physics, chemistry, and even economics. - What are the benefits of using dimensional analysis?
Using dimensional analysis helps catch errors, simplify calculations, and deepen our understanding of relationships between quantities.

conclusion :
Let’s dive into the topic of units of measurement and dimensional analysis:
Units of measurement play a crucial role in our everyday lives, helping us communicate and understand the physical world around us. They provide a standardized way to express quantities such as length, time, mass, and more. For example, when we say something is 2 meters long, we all have a clear understanding of its size. Without units, it would be challenging to compare and communicate measurements accurately.
Now, let’s talk about dimensional analysis. It’s like a superpower that allows us to check the consistency and accuracy of equations by examining the units involved. By analyzing the dimensions of different quantities in an equation, we can catch errors and ensure that the equation makes sense. For instance, if we’re solving a problem involving velocity, we can use dimensional analysis to confirm that the equation includes the correct units of distance and time. This process not only helps us avoid mistakes but also deepens our understanding of the relationships between different quantities.
Post Comment