Chapter #10: Simple Harmonic Motion and Waves -

Introduction:

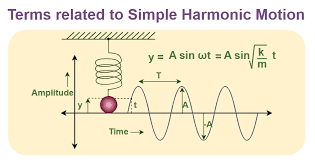
Simple Harmonic Motion (SHM). It’s a fascinating concept in physics that describes the repetitive back-and-forth motion of an object around a stable equilibrium position.

Imagine a mass attached to a spring. When the mass is displaced from its equilibrium position and then released, it starts oscillating back and forth. This motion is periodic, meaning it repeats itself over time. The key characteristic of SHM is that the restoring force acting on the object is directly proportional to its displacement from the equilibrium position and is always directed towards that position. This gives rise to a sinusoidal pattern of motion.

Example:

To explain it step by step, let’s consider an example of a pendulum. When you pull a pendulum to one side and release it, it swings back and forth. The force of gravity acts as the restoring force, always pulling the pendulum towards its equilibrium position. As it swings, the pendulum oscillates between two extreme points, known as the amplitude. The time it takes for one complete back-and-forth motion is called the period, and the number of oscillations per unit of time is called the frequency.

Now, let’s dive into some frequently asked questions about Simple Harmonic Motion:

What is the formula for the period of SHM?
The formula is T = 2π√(m/k), where T is the period, m is the mass, and k is the spring constant.
How does the amplitude affect the motion?
The amplitude determines the maximum displacement from the equilibrium position. A larger amplitude leads to a wider swing or oscillation.
Can SHM occur without a restoring force?
No, SHM requires a restoring force that acts in the opposite direction of the displacement to bring the object back to equilibrium.
What factors affect the frequency of SHM?
The frequency is influenced by the mass of the object and the stiffness of the restoring force (spring constant).
Can SHM occur in other systems besides springs and pendulums?
Yes, SHM can occur in various systems, such as vibrating strings, oscillating atoms, and even some biological systems.
What is the relationship between SHM and circular motion?
SHM can be thought of as the projection of circular motion onto a straight line. The oscillatory motion is related to the circular path of an object.
- How does damping affect SHM?
  Damping refers to the presence of external forces that reduce the effect.

Summary

Simple harmonic motion (SHM) is an oscillatory motion where acceleration is proportional to displacement from the mean position and directed towards it.
SHM examples: mass-spring systems, simple pendulums, and a ball in a bowl.
A pendulum’s time is the duration to complete one cycle, dependent on its length but not on mass or amplitude.
Frequency is the number of cycles per second, reciprocal to the time.
Amplitude is the maximum displacement from the mean position in SHM.
Waves transfer energy without moving matter.
Mechanical waves require a medium for propagation.
Electromagnetic waves do not need a medium for propagation.
Transverse waves: medium particles vibrate perpendicular to wave direction.
Longitudinal waves: medium particles vibrate parallel to the wave direction.
Wave speed (v) equals frequency (f) times wavelength (λ): v = fλ.
A ripple tank demonstrates water waves’ properties, such as reflection, refraction, and diffraction.
Reflection: Waves bounce back into the original medium upon hitting another medium’s surface.
Refraction: Waves change direction when entering a different medium; speed and wavelength change, but frequency remains constant.
Diffraction: Waves bend around obstacles or sharp edges.

10.1 Simple Harmonic Motion

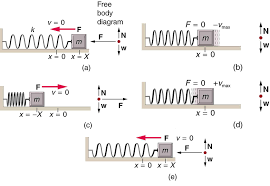
Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement. Mathematically, this can be expressed as: F=−kxF = -kxF=−kx where FFF is the restoring force, kkk is the spring constant, and xxx is the displacement from the equilibrium position.

Necessary Conditions for SHM:

There must be a restoring force that acts to bring the object back to its equilibrium position.
The magnitude of the restoring force must be proportional to the displacement from the equilibrium position and opposite in direction.

10.2 Examples of Simple Harmonic Motion

The motion of a mass attached to a spring.
The oscillation of a pendulum for small angles.
The vibration of a tuning fork.
The child’s motion on a swing (approximated as SHM for small amplitudes).

10.3 Damped Oscillations

Damped Oscillations are oscillations in which the amplitude decreases over time due to energy loss (e.g., friction or air resistance). The damping force is typically proportional to the velocity of the oscillating body but acts in the opposite direction.

How Damping Reduces Amplitude:

As the system oscillates, the damping force dissipates energy, usually as heat.
This loss of energy results in a gradual decrease in the oscillation amplitude until the system eventually comes to rest.

10.4 Definition of a Wave

A wave is a disturbance that transfers energy from one place to another without transferring matter.

Difference between Mechanical and Electromagnetic Waves:

Mechanical Waves: Require a medium to travel through (e.g., sound waves, water waves).
- Example: Sound waves in air.
Electromagnetic Waves: Do not require a medium and can travel through a vacuum (e.g., light waves, radio waves).
- Example: Light waves from the sun.

10.5 Longitudinal vs. Transverse Waves

Longitudinal Waves: The particles of the medium move parallel to the direction of wave propagation.
- Example: Sound waves.
Transverse Waves: The particles of the medium move perpendicular to the direction of wave propagation.
- Example: Light waves, waves on a string.

10.6 Drawing a Transverse Wave

Below is a drawing of a transverse wave with an amplitude of 2 cm and a wavelength of 4 cm.

bash

Copy code

2 cm | /\ | / \ | / \ | / \ | / \ 0 cm ---/----------\---- / \ -2 cm / \ / \

Crest: The highest point of the wave.
Trough: The lowest point of the wave.

10.7 Relationship between Velocity, Frequency, and Wavelength

The velocity (vvv) of a wave is related to its frequency (fff) and wavelength (λ\lambdaλ) by the equation: v=fλv = f \lambdav=fλ

The period (TTT) is the reciprocal of the frequency: T=1fT = \frac{1}{f}T=f1

So, the velocity can also be expressed as: v=λTv = \frac{\lambda}{T}v=Tλ

10.8 Energy Transfer in Waves

Waves Transfer Energy without Matter Transfer: An experiment demonstrating this can be a simple ripple tank experiment. When you disturb the water surface at one point, ripples (waves) spread out in concentric circles. If you place a small floating object on the water, it will move up and down as the waves pass by but do not travel with the waves. This shows that energy is transferred through the water, but the water particles and the floating object do not travel with the wave.

10.9 Properties of Waves in a Ripple Tank Experiment

Reflection: When waves hit a barrier, they bounce back. The angle of incidence equals the angle of reflection.
Refraction: When waves move from one medium to another (e.g., deep to shallow water), their speed changes, causing the wave direction to change.
Diffraction: When waves pass through a small opening or around obstacles, they spread out.

10.10 Relationship between Frequency and Wavelength

Increasing the frequency of a wave decreases its wavelength if the wave velocity remains constant. They are inversely related: λ=vf\lambda = \frac{v}{f}λ=fv

Conceptual Questions

10.1 Effect of Doubling the Length of a Pendulum on its Time Period: T=2πLgT = 2\pi \sqrt{\frac{L}{g}}T=2πgL Doubling the length LLL increases the time period TTT by a factor of 2\sqrt{2}2.

10.2 Is the Bouncing Ball’s Motion Simple Harmonic? No, the motion of a bouncing ball is not SHM because the restoring force is not proportional to the displacement in a harmonic manner, and energy is lost with each bounce.

10.3 Pendulum with Different Mass Bobs: The period of a simple pendulum is independent of the mass of the bob. It only depends on the length of the string and the acceleration due to gravity.

10.4 Waves That Do Not Require a Medium: Electromagnetic waves do not require a material medium for propagation.

10.5 Speed Change in Waves Moving from Deep to Shallow Water: When waves move from deep to shallow water, their speed decreases because the wavelength decreases while the frequency remains constant.

FAQs

Q: What is simple harmonic motion (SHM)?

A: SHM is an oscillatory motion where the acceleration of a body is directly proportional to its displacement from the mean position and always directed towards it.

Q: What factors affect the time period of a simple pendulum?

A: The time period of a simple pendulum depends on its length and is independent of the mass and amplitude.

Q: What is the difference between mechanical and electromagnetic waves?

A: Mechanical waves require a medium for propagation, while electromagnetic waves do not.

Q: How do transverse and longitudinal waves differ?

A: In transverse waves, particles vibrate perpendicular to the wave direction. In longitudinal waves, particles vibrate parallel to the wave direction.

Q: What happens during wave reflection and refraction?

A: Reflection occurs when a wave bounces back into its original medium after hitting another medium’s surface. Refraction occurs when a wave changes direction upon entering a different medium, altering its speed and wavelength but not frequency.

Q: What is wave diffraction?

A: Diffraction is the bending of waves around obstacles or sharp edges.

References

“Simple Harmonic Motion – Concepts”.

Fowles, Grant R.; Cassiday, George L. (2005). Analytical Mechanics (7th ed.). Thomson Brooks/Cole. ISBN 0-534-49492-7.
Taylor, John R. (2005). Classical Mechanics. University Science Books. ISBN 1-891389-22-X.
Thornton, Stephen T.; Marion, Jerry B. (2003). Classical Dynamics of Particles and Systems (5th ed.). Brooks Cole. ISBN 0-534-40896-6.
Walker, Jearl (2011). Principles of Physics (9th ed.). Hoboken, New Jersey: Wiley. ISBN 978-0-470-56158-4.

Chapter #10: Simple Harmonic Motion and Waves